87

Terminologie et concepts mis en oeuvre

3.2.2.2 Du point de vue mathématique

Pour formaliser ce que l'on vient de dire, donnons les définitions suivantes :

SoientW = {w₁,...,w_n}, l'ensemble des spécimens ou individus observés,
P [!] W, l'ensemble de tous les individus observables,
P(W), l'ensemble des parties de la population observée W.

Soit F, une fonction de représentation de P--> O, O désignant l'espace d'observation, qui à chaque individu observable wde Pfait correspondre sa description potentielle y(w) = d [!] O :

F :P[!]
wa

O
F(w)

Soit y, une fonction de représentation de W--> D, Ddésignant l'espace de description des individus observables (D = F(P) [!] O), qui à chaque individu observé w de Wfait correspondre sa description d = y(w)[!] D :

y :W[!]
wa

D
y(w)

Soit une classe observée C [!]P(W). Pour chacune, on peut associer une définition D = y(C), D [!]P(D). En notant b_Dla fonction d'appartenance à la classe D :

[^0,1
]
1 si d[!]

bD:D[!]
da

D,0 sinon

D représente la somme (ou disjonction) des descriptions observées de chaque individu de la classe : D = [!]d. d [!]D est aussi appelé un exemple de la classe D, un contre-exemple est donc un élément de D\D.

On obtient ainsi le schéma de la figure 3.3 présenté dans [Diday, 1993] :

[0,1]

W

D
Fig. 3.3 : Le triangle des fonctions entre individus et leurs descriptions

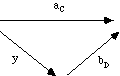
avec la propriété : " w [!] W, a_C(w) = b_D(y (w)) = b_D o y (w)