62

Chapitre 2

[!] [!]

indépendance des événements liés aux attributs (variables explicatives), tirage au hasard des individus de l'échantillon étudié (échantillonnage aléatoire) dans une population nombreuse et déterminée.

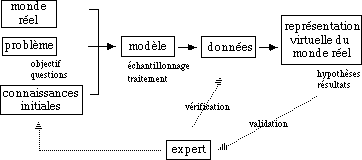
Certains statisticiens ont néanmoins une vision plus dynamique de la robustesse : pour Tomassone (1991), la Statistique est un guide pour toute démarche scientifique expérimentale. Elle demande de s'impliquer totalement dans l'analyse d'un monde "réel" incomplet et flou pour aboutir à sa représentation "virtuelle" obligatoirement schématique. Appliquer la Statistique requiert un assemblage ad hocde trois composants : un Objectif, un Modèle, des Données.

L'objectif O correspond à un ensemble de questions auxquelles la Statistique est capable de répondre. Pour O fixé (ex : classification de plusieurs populations en classes homogènes), il existe au moins un modèle M qui permet de l'atteindre. Par modèle M, il faut comprendre deux éléments : une technique de sélection des données D (échantillonnage, plan d'expérience) et une technique de traitement des données quand on les aura acquises. Simultanément, un modèle M a besoin de certaines données D pour pouvoir être appliqué. Pour un utilisateur, il est indispensable de savoir quelles données D sont nécessaires pour utiliser M, et donc pour atteindre l'objectif O qu'il s'est fixé.

Pour ces statisticiens, la robustesse liée à l'acceptation du résultat découle d'un va-et-vient entre M et D autour de O fixé(figure 2.1). Cette robustesse est provisoire tant que des éléments nouveaux ne viennent pas contredire le résultat précédemment acquis.

Fig. 2.1 : La robustesse dans la démarche statistique [Tomassone, 1991]