218

Chapitre 7

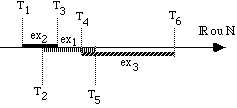
Néanmoins, pour le calcul du gain d'information de chaque seuil, le problème est ici plus délicat du fait du recouvrement des intervalles entre les différents exemples : le même exemple peut être comptabilisé deux fois pour un seuil donné : A(Ex) <= T_iet A(Ex) >= T_i. Mais cela ne gêne pas le calcul du gain d'information lorsque les modalités ne sont pas disjointes(un individu peut prendre plus d'une modalité pour la variable A), de même que lorsqu'elles ne sont pas exhaustives(un individu peut ne pas prendre une modalité de la variable, ce qui est le cas de la réponse «inconnu»).

En effet, que ce soit pour une variable numérique où le test est binarisé (n = 2 branches ou valeurs possibles) ou pour une variable nominale n_aire, si la valeur de A est inconnue pour un exemple, alors toutes les valeurs sont possibles : l'exemple est propagé sur les n branches. Par contre, si l'exemple possède plusieurs valeurs résultant de l'imprécision des descriptions observées de l'observateur (voir § 3.6.10.2), il est propagé sur ces branches uniquement. Afin que la mesure du gain d'information reste consistante, la taille du sous- ensemble E au noeud d est artificiellement modifiée :

Card (E) = Card (E) + (p - 1), ou p est le nombre de branches ou l'exemple a été propagé.

Remarques: Dans [Fayyad & Irani, 1992], il est montré qu'il est inutile de calculer le gain d'information des (n - 1) points possibles de la partition engendrée par les n valeurs d'un attribut numérique : il suffit de ne considérer que les seuils qui séparent deux classes différentes après avoir trié les exemples par ordre croissant. Cette fonctionnalité n'est pas encore implantée dans l'algorithme.

Par contre, un attribut de type entier ou réel, s'il est choisi à un noeud de l'arbre, peut être réutilisé dans la liste des tests possibles pour engendrer le sous-arbre du noeud (contrairement aux autres tests non numériques qui sont éliminés de la liste). Les valeurs possibles de ce nouveau test ont alors un sous espace d'observation O' restreint et déterminé par le calcul du seuil du test initial.

Pour une étude de la complexité globale de l'algorithme, on peut se reporter à [Manago, 1988], [Crémilleux, 1991].