210

Chapitre 7

Fig. 7.1 : Schéma d'un noeud de l'arbre T Soit A = yⁱ
j^{, un attribut d'une partie de la} description et n descriptions ou valeurs de cet attribut {v₁,...,v_i,...,v_n},

v_i

= v

k

instance k

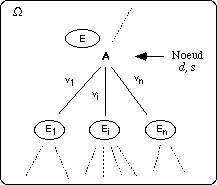
Une fonction de partitionnement R induisant une partition sur E est définie de la manière suivante :

[!]

R : " w [!] E , A(w) = v_i

w [!] E_i

R (E) = {E₁,...,E_n} est alors une partition de E avec les propriétés suivantes :
E = [!]E_i
"i = 1,...,n on a E_i[!]E_j= [!]

7.1.3 Algorithme

On peut décrire notre algorithme par une procédure générale de construction d'arbre de décision [Vignes, 1992].

Cela consiste à sélectionner un attribut selon un certain critère pour former le premier noeud de l'arbre, puis à créer les différentes branches qui partent de ce noeud, une branche étant étiquetée par l'une des valeurs possibles de l'attribut sélectionné. Ensuite, on répartit la liste des exemples restants en fonction de leur compatibilité avec chaque branche au noeud courant. Enfin, on réitère le processus jusqu'à n'obtenir que des exemples de la même classe quiforment alors une feuille de l'arbre de décision.