213

Le traitement des descriptions biologiques: KATE et CaseWork

les vingts participants nous sont entièrement inconnus ou de donner le numéro du billet de loterie gagnant du gros lot au prochain tirage...
Le degré d'incertitude de chaque expérience est déterminé par le nombre k d'issues possibles ainsi que de leurs probabilités d'apparition : elle est notée f(k). Cette fonction est déterminée par les trois propriétés suivantes:

1) 2)

3)

Si k = 1, il n'y a aucune incertitude dans ce cas et la mesure doit s'annuler. Lorsque k augmente, la mesure f(k) est une fonction croissante des k issues.
Si l'on considère deux expériences indépendantes aet b(avec k issues pour aet l issues pour b), le degré d'incertitude de l'expérience composée abest égal à la somme des incertitudes qui caractérisent les expériences aet b: f(kl) = f(k) + f(l).

On peut montrer [Guiasu & Theodorescu, 1971] que la seule fonction de la variable k qui vérifie ces trois conditions est la fonction logarithmique : f(k) = log k. Dans les applications, les logarithmes de base 2 sont le plus souvent utilisés, ce qui signifie que l'on prend comme unité de mesure du degré d'incertitude, l'incertitude d'une expérience possédant deux issues également probables. Ce choix n'est pas essentiel : un facteur constant existe entre les différentes bases.

Cette mesure est aussi une information sur la capacité d'un attribut à séparer efficacement les exemples. Supposons en effet un attribut ayant 2 valeurs possibles, p₁et p₂sont les proportions d'exemples prenant respectivement les valeurs 1 et 2. Si tous les exemples d'apprentissage prennent la première valeur (p₁= 1 et p₂= 0), alors le fait d'observer l'état 1 n'apporte aucune information supplémentaire pour séparer les exemples. Inversement, si la répartition des exemples selon les valeurs de l'attribut est homogène (p₁= 1/2 et p₂= 1/2 pour l'équi-répartition), l'efficacité de discrimination est maximale.

On peut donc associer à chaque attribut A[!] Y_dune entropie Ent(E) qui est la somme des distributions de probabilités desn valeurs de son domaine de définition. Ces probabilités sont calculées en fonction des états que prennent les exemples pour l'attribut A.

Pour chaque valeur discrète de A, on définit la fréquence d'occurrence P_ide E_i qui est la probabilité associée à chaque valeur d'attribut pour qu'un exemple w appartenant à E appartienne à E_i:

Pi=
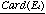
Card(E)^{est donc la probabilité de choisir un exemple ayant l'état i de A.}

[!]ⁿ
Ent ( E ) = -Pi[!]log2Pi
i =1

L'entropie est alors calculée selon la formule :